Varieties
Foxes
V - Chocolate Fox (cc/f)
at/at bc/* cch/cch D/* P/*
at/a bc/* cch/cch D/* P/*
Other possible genotypes:
at/at bc/* cch/ce D/* P/*,
at/a bc/* cch/ce D/* P/* ("mock chocolate-fox")
at/at bc/* ce/ce D/* P/*,
at/a bc/* ce/ce D/* P/* (very dark Coffee fox)
"Eyes black. The colour should be that of plain (not milk) chocolate and should be rich, deep and full of life. Feet, sides and rump only to be ticked with white hairs. Belly white."
Breeding information below the pictures.
Note: This article is old and waiting to be rewritten.
Quick Look
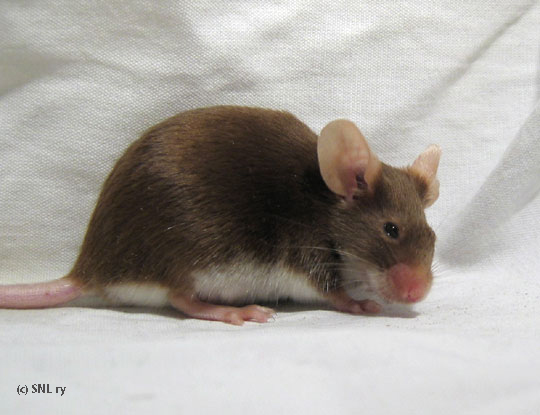
For a starting point, see black fox. Once there are black fox mice to work with, the white fox belly can be bred into chocolate top color by using chocolate tans. Beware of using chocolate fox "lookalikes", like dark Coffee fox (at/* B/* ce/ce) or the kind pictured above, as you'd be up to some surprises with them.
A Little Closer Look
In order to breed chocolate foxes, you need to combine black-and-tan gene (at), chinchilla dilution (cch) and chocolate dilution (bc) into the same animal. The first one is easy, as black-and-tan is dominant over a. The second two are recessives in their own loci. The preferrable first combination is black fox (the source for the chinchilla dilution, already has the black-and-tan) and chocolate tan (which has the tan and the needed chocolate dilution). You can, of course, go the harder route and mate a chinchilla, but this combination would make it necessary to try and get rid of A (or even Aw), so it isn't a recommended one.
This first combination would bring you (unless the black fox carries chocolate and/or the chocolate tan carries one of the many c-locus recessives) black tans carrying both the chinchilla dilution and chocolate dilution (the F1 generation).
Mating two F1 mice together (which would give you the F2 generation) would in theory bring you:
- 9/16 black tan (1 x B/B C/C, 1 x B/B C/cch, 3 x B/bc C/C, 4 x B/bc C/cch)
- 3/16 black fox (1 x B/B cch/cch, 2 x B/bc cch/cch
- 3/16 chocolate tan (1 x bc/bc C/C, 2 x bc/bc C/cch)
- 1/16 chocolate fox (at/* bc/bc cch/cch).
In practice you can get any number of any of the possible outcomes. What makes things interesting (read: difficult) is that you can't see from just looking at the mouse, whether a black tan young carries chinchilla dilution, chocolate dilution, both or none; whether a black fox young carries the chocolate dilution or not, or whether a chocolate tan young carries the chinchilla dilution. If the original parents were at/a instead of at/at, you'll get some Sepias (a/a cch/cch) and chinchillated chocolates as well. You can lower the risk of getting these by not using any possible F1-self blacks.
As you can see, creating chocolate foxes from scratch isn't quick. That's why they aren't usually specifically bred for, but are more of a side product of black fox breeding. Once there are chocolate foxes available, it's just a question of breeding them together in order to get more.